Cours NSI-SNT
Représentation des entiers relatifs
Méthode naïve: utilisation d’un bit de signe
La façon la plus simple de procéder serait de réserver le bit de poids fort pour le signe (0 pour positif et 1 pour négatif), et de garder le reste pour la représentation de la valeur absolue du nombre.
Avec un codage utilisant des mots de \(n\) bits, on pourrait représenter des nombres entre \(-2^{n-1} + 1 \text{ et } 2^{n-1} - 1\).
Par exemple, avec un codage sur 3 bits, des nombres entre -3 et 3:
| Représentation binaire | Valeur décimale |
|---|---|
| 000 | +0 |
| 001 | +1 |
| 010 | +2 |
| 011 | +3 |
| 100 | -0 |
| 101 | -1 |
| 110 | -2 |
| 111 | -3 |
Mais alors ? Pourquoi pas cette méthode ? 🤔
Malheureusement cette représentation possède deux inconvénients. Le premier (mineur) est que le nombre zéro (0) possède deux représentations. L’autre inconvénient (majeur) est que cette représentation impose de modifier l’algorithme d’addition ; si un des nombres est négatif, l’addition binaire usuelle donne un résultat incorrect.
Seconde méthode: Complément à 2
La représentation d’un nombre entier relatif se fait avec un nombre de bits définit à l’avance.
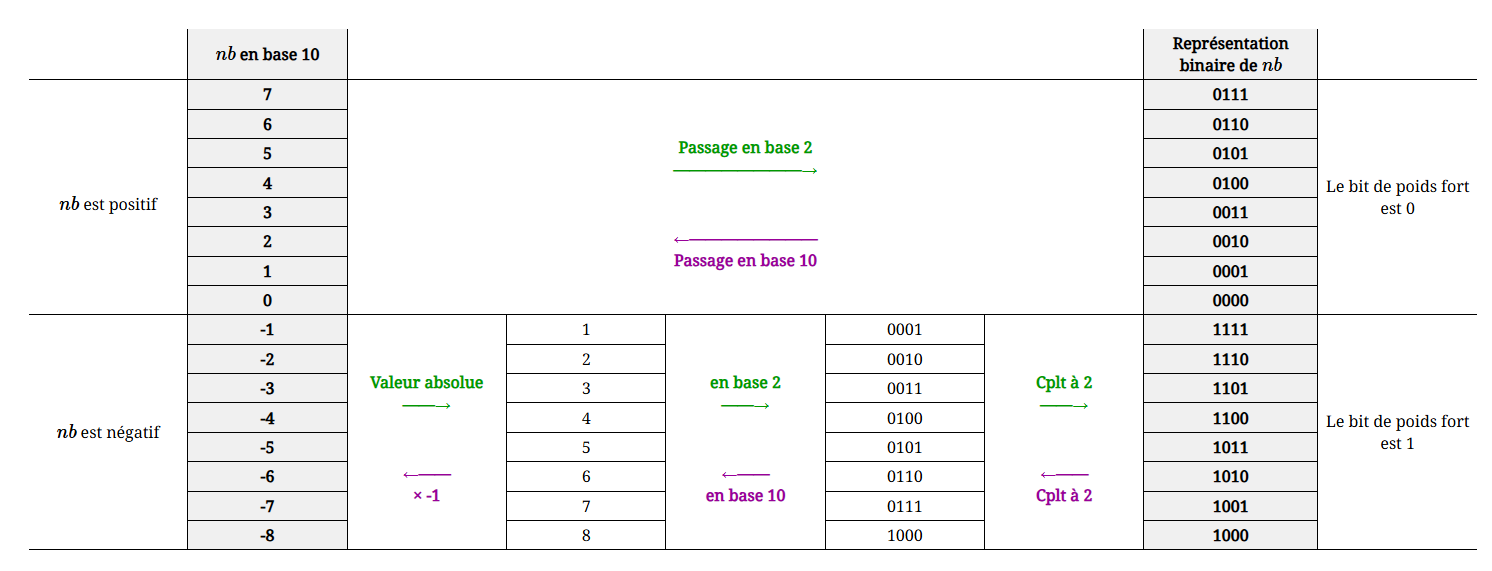
Exemple avec 4 bits
Avec 4 bits, on dispose de \(2^4 = 16\) valeurs.
On choisit de représenter les entiers relatifs de \(-8\) à \(7\).
Méthodologie
Première Méthode : ( à connaître )
L’obtention du complément à 2 d’un nombre binaire se fait en deux étapes :
- on inverse tous les bits
- on ajoute 1
C’est tout ! 😱
Exemple
La valeur −1 a pour valeur absolue 1 codé
001sur 3 bits. On inverse les bits:110On ajoute 1 :111
Deuxième Méthode ( pas à connaître, mais pratique )
L’entier négatif \(x\) est codé comme s’il s’agissait de l’entier \(x+2^n\) ou n est la taille du mot binaire.
Exemple
Je prend -1 en représentation décimal que je souhaite encoder sur 3 bits J’applique la formule en remplaçant x par -1 et n par 3 -> \(-1 + 2^3\) qui donne 7 en base décimal Je retranscris 7 en base 10 en base deux ->
111
Remarque : Le bit de poids fort de la représentation d’un entier positif est toujours 0, alors que celui d’un nombre entier négatif est toujours 1.
Applications
Application I
Dans toutes cette partie, on travaillera sur 8 bits.
1) Combien d’entiers relatifs peut-on représenter ? En donner la liste ?
2) Donner les représentations binaires en complément à 2 des nombres 125 et -125.
3) Donner les valeurs décimales des nombres dont les représentations binaires en complément à 2 sont les suivants :
a) 1111 1111
b) 0000 0000
c) 1001 1001
d) 0110 01114) On s’intéresse au nombre relatif dont la représentation binaire en complément à 2 est 1010 0101
a) Ce nombre est-il positif ou négatif ? b) Donner la représentation binaire de l’opposé de ce nombre.
Application II : Additionner des entiers relatifs
Dans toutes cette partie, on travaillera sur 6 bits.
1) Combien d’entiers relatifs peut-on représenter ? En donner la liste ?
2) Donner la représentation binaire en complément à 2 des entiers relatifs -18 et -12.
3) A l’aide d’une addition en binaire, trouver la représentation binaire en complément à 2 de la somme de -18 et -12.
4) Cette addition est-elle correcte (détailler la démarche).
Application III : Encore plus d’additions !
Faire les opérations suivantes sur 8 bits et interpréter le résultat :
1)
01001001(73) +11101110(-18)2)
00101101(45) +11010111(-41)3)
11110000(-16) +00001111(15)4)
01111111(127) +00000001(1)🐍 Application IV :
Écrire une fonction
to_binary(n, b)qui prend un entier n (positif ou négatif) et retourne sa représentation binaire sur b bits en complément à 2.Exemple :
>> print(to_binary(5, 8)) "00000101" >> print(to_binary(-5, 8)) "11111011"🐍 Application V :
Écrire une fonction
addition_binaire(n, m, b)qui prend deux entiers n et m ainsi que leur représentation binaire sur b bits et les additionnes et retourne le résultat de l’addition.Exemple :
>> print(addition_binaire(-1, 3, 3)) "010"